This question has been taken from Book:- ML aggarwal, Avichal publication, class10th, quadratic equation in one variable, chapter 5, exercise 5.5
This is an important ques
(i) Harish made a rectangular garden, with its length 5 metres more than its width. The next year, he increased the length by 3 metres and decreased the width by 2 metres. If the area of the second garden was 119 sq m, was the second garden larger or smaller ?
(ii) The length of a rectangle exceeds its breadth by 5 m. If the breadth were doubled and the length reduced by 9 m, the area of the rectangle would have increased by 140 m². Find its dimensions.
Question no.15 , ML Aggarwal, chapter 5, exercise 5.5, quadratic equation in one variable, ICSE board,




Solution:(i)
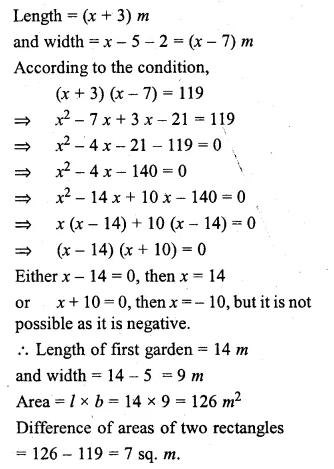
In first case,
Let length of the garden = x m
then width = (x – 5) m
Area = l x b = x(x – 5) sq. m
In second case,
(ii) In first case:
Let us consider length of the rectangle be ‘x’ meter
Width = (x – 5) meter
Area = lb
= x(x – 5) sq.m
In second case:
Length = (x – 9) meter
Width = 2 (x – 5) meter
Area = (x – 9) 2(x – 5) = 2(x – 9) (x – 5) sq.m
So according to the question,
2(x – 9) (x – 5) = x(x – 5) + 140
2(x2 – 14x + 45) = x2 – 5x + 140
2x2 – 28x + 90 – x2 + 5x – 140 = 0
x2 – 23x – 50 = 0
let us factorize,
x2 – 25x + 2x – 50 = 0
x(x – 25) + 2 (x – 25) = 0
(x – 25) (x + 2) = 0
So,
(x – 25) = 0 or (x + 2) = 0
x = 25 or x = -2
∴ Length of the first rectangle = 25meters. [Since, -2 is a negative value]
Width = x – 5 = 25 – 5 = 20meters
Area = lb
= 25 × 20 = 500 m2