Sir give me the best solution for the question of class 10th ncert math of Applications of Trigonometry chapter of exercise 9.1 of question no.11, how i solve this problem in easy way A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.
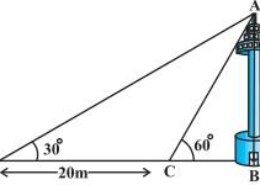
Given, AB is the height of the tower.
DC = 20 m (given)
As per given diagram, In right ΔABD,
tan 30° = AB/BD
1/√3 = AB/(20+BC)
AB = (20+BC)/√3 … (i)
Again,
In right ΔABC,
tan 60° = AB/BC
√3 = AB/BC
AB = √3 BC … (ii)
From equation (i) and (ii)
√3 BC = (20+BC)/√3
3 BC = 20 + BC
2 BC = 20
BC = 10
Putting the value of BC in equation (ii)
AB = 10√3
This implies, the height of the tower is 10√3 m and the width of the canal is 10 m.