Yesterday i was doing this question but i can’t able to able to solve this problem, how i solve this problem in easy and simple way of question no.12 of exercise 15.1 of probability chapter, give me the best way for answering this question A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see Fig. 15.5), and these are equally likely outcomes. What is the probability that it will point at (i) 8? (ii) an odd number? (iii) a number greater than 2? (iv) a number less than 9?
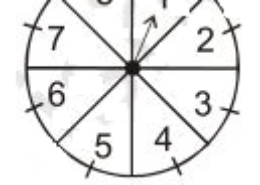
Total number of possible outcomes = 8
P(E) = (Number of favourable outcomes/ Total number of outcomes)
(i) Total number of favourable events (i.e. 8) = 1
∴ P (pointing at 8) = ⅛ = 0.125
(ii) Total number of odd numbers = 4 (1, 3, 5 and 7)
P (pointing at an odd number) = 4/8 = ½ = 0.5
(iii) Total numbers greater than 2 = 6 (3, 4, 5, 6, 7 and 8)
P (pointing at a number greater than 4) = 6/8 = ¾ = 0.75
(iv) Total numbers less than 9 = 8 (1, 2, 3, 4, 5, 6, 7, and 8)
P (pointing at a number less than 9) = 8/8 = 1