How i solve the problem of exercise 6.3 of class 10th math, of chapter Triangles, How i solve in easy way Please help me sir for solving this problem Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR (see Fig 6.41). Show that ΔABC ~ ΔPQR.
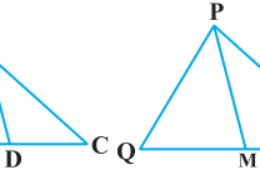
Given, ΔABC and ΔPQR, AB, BC and median AD of ΔABC are proportional to sides PQ, QR and median PM of ΔPQR
i.e. AB/PQ = BC/QR = AD/PM
We have to prove: ΔABC ~ ΔPQR
As we know here,
AB/PQ = BC/QR = AD/PM
⇒AB/PQ = BC/QR = AD/PM (D is the midpoint of BC. M is the midpoint of QR)
⇒ ΔABD ~ ΔPQM [SSS similarity criterion]
∴ ∠ABD = ∠PQM [Corresponding angles of two similar triangles are equal]
⇒ ∠ABC = ∠PQR
In ΔABC and ΔPQR
AB/PQ = BC/QR ………………………….(i)
∠ABC = ∠PQR ……………………………(ii)
From equation (i) and (ii), we get,
ΔABC ~ ΔPQR [SAS similarity criterion]