what is the tricky way for solving the question of class 9th ncert math of Areas of Parallelograms and Triangles chapter of ncert of exercise 9.4 of math give me the best and simple way for solving this question in easy and simple way In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ^ DE meets BC at Y. Show that:(i) ΔMBC ≅ ΔABD
AnilSinghBoraGuru
In Fig. 9.34, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ^ DE meets BC at Y. Show that:(i) ΔMBC ≅ ΔABD Q.8(1)
Share



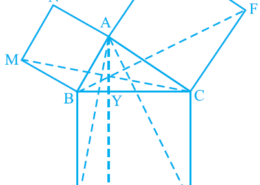

We know that each angle of a square is 90°. Hence, ∠ABM = ∠DBC = 90º
∴∠ABM+∠ABC = ∠DBC+∠ABC
∴∠MBC = ∠ABD
In ∆MBC and ∆ABD,
∠MBC = ∠ABD (Proved above)
MB = AB (Sides of square ABMN)
BC = BD (Sides of square BCED)
∴ ∆MBC ≅ ∆ABD (SAS congruency)