This is the basic and conceptual question from similarity chapter in which we are to find
(i) length of BP
(ii) the ratio of areas of △APB and △DPC.
And we have given a figure of trapezium in which it’s parallel sides are AB and DC
ML Aggarwal Avichal Publication Class 10, Chapter 13.3, question no 14a



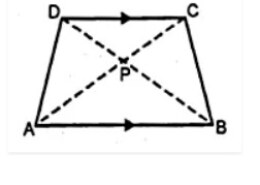

From the question it is given that,
DC is parallel to AB
AB=9cm,DC=6cm and BB=12cm
(i) Consider the △APB and △CPD
∠APB=∠CPD … [because vertically opposite angles are equal]
∠PAB=∠PCD … [because alternate angles are equal]
So, △APB∼△CPD
Then, BP/PD=AB/CD
BP/(12−BP)=9/6
6BP=108−9BP
6BP+9BP=108
15BP=108
BP=108/15
Therefore, BP=7.2cm
(ii) We know that, area of △APB/area of △CPD=AB2/CD2
area of △APB/area of △CPD=92/62
area of △APB/area of △CPD=81/36
By dividing both numerator and denominator by 9, we get,
area of △APB/area of △CPD=9/4
Therefore, the ratio of areas of △APB and △DPC is 9:4.